TEXED es una interfaz gráfica para la edición y vista previa de las ecuaciones de LaTeX para su uso en MATLAB. La principal diferencia entre las dos entradas es la capacidad de éste para devolver la cadena de TeX que el usuario hubiera hecho a mano a través de la interfaz gráfica de usuario, y el contenido de zip.
D.E.S.C.A.R.G.A.R
videotutoriales de matlab, octave, numpy, python, POA, algoritmia, simulacion de procesos en ingenieria quimica, y algo de ingenieria quimica
martes, 3 de diciembre de 2013
miércoles, 27 de noviembre de 2013
jueves, 21 de noviembre de 2013
Integrales definidas e Indefinidas en Matlab
>> %Integrales en Matlab >> %Integral indefinida >> syms >> syms x >> f= 2*x^4; >> F = int(f) F = (2*x^5)/5 >> %integral definida >> F = int(f,3,2) F = -422/5 >> %integrales impropias (al infinito) >> D = (exp(-x)*sin(x))/x D = (exp(-x)*sin(x))/x >> pretty (D) exp(-x) sin(x) -------------- x >> DD =int(D,0,inf) DD = pi/4 >> DD =int(D) DD = (ei(x*(- 1 - i))*i)/2 - (ei(x*(- 1 + i))*i)/2 >> pretty(DD) ei(x (- 1 - i)) i ei(x (- 1 + i)) i ----------------- - ----------------- 2 2 >>
sábado, 16 de noviembre de 2013
jueves, 7 de noviembre de 2013
lunes, 28 de octubre de 2013
Métodos numéricos con Matlab
Este texto introduce al lector a una amplia gama de algoritmos numéricos, mientras que explica los principios fundamentales e ilustra las aplicaciones de esos algoritmos.
=D.E.S.C.A.R.G.A.R=
=D.E.S.C.A.R.G.A.R=
jueves, 24 de octubre de 2013
lunes, 21 de octubre de 2013
Modelo de reacciones en serie, usando Matlab
Tenemos la función en la que planteamos nuestras ecuaciones de balance.
Ahora este es nuestro programa principal, en el cual usamos en este caso la función serie donde tenemos nuestra ecuación plantead como dEct.%Modelo basico de reacciones en serie %esta funcion debe llamarse serie %x---k1-->y---k2--->z function dEct = serie(t,C) global k1 k2 dEct = [-k1*C(1);k1*C(1)-k2*C(2);k2*C(2)];
Corriendo la aplicacion.%programa principal clc clear global k1 k2 disp('Introduce los siguientes Datos') Cxo = input('Concentracion inicial de X (mol):_ '); Cyo = input('Concentracion inicial de Y (mol):_ '); Czo = input('Concentracion inicial de Z (mol):_ '); cuadal = input('Cuadal (l /min):_ '); k1 = input('K1:_ '); k2 = input('K2:_ '); tiempolimite = input('Tiempo maximo de reaccion:_ '); vectiempo = [0:0.0005:tiempolimite]; vecC = [Cxo Cyo Czo]; [t,C]= ode45('serie',vectiempo,vecC); plot(t,C(:,1),'-',t,C(:,2),':',t,C(:,3),'--'); xlabel('tiempo (min)'); ylabel('Concentracion (mol/litro)'); title('Modelo de Reaccion en Serie'); legend ('Cx','Cy','Cz'); Cmax = max(C(:,2)); tmax = t(find(C(:,2)==(max(C(:,2))))); Vol = cuadal*tmax
Introduce los siguientes Datos Concentracion inicial de X (mol):_ 3.5 Concentracion inicial de Y (mol):_ 1.23 Concentracion inicial de Z (mol):_ 0 Cuadal (l /min):_ 28.598 K1:_ 0.562 K2:_ 0.123 Tiempo maximo de reaccion:_ 25 Vol = 83.2488
jueves, 17 de octubre de 2013
Derivadas en Matlab.
Seguimos con las publicaciones de Matlab para calculo, ahora toca el tema de derivadas.
>> syms x >> f = 2*x^2; >> %procedemos a derivarla mendiante el comando diff() >> diff(f) ans = 4*x >> %% DERIVADA PARCIAL >> syms y >> F= 2*x^3*y; >> diff(F,x)% con respecto a X ans = 6*x^2*y >> diff(F,y)% con respecto a Y ans = 2*x^3 >> % las letras que son consideras literales son: x,w,y,z >> %todas las demas letras son consideradas constantes >> syms a >> f2 = 3*a*x^2 f2 = 3*a*x^2 >> diff(f2) ans = 6*a*x >> syms x n >> f3 = x^n; >> diff (f3) ans = n*x^(n - 1) >> f3 = sqrt(x^n); >> F2 = diff(f3) F2 = (n*x^(n - 1))/(2*(x^n)^(1/2)) >> % si nos damos cuenta tenemos en estos 2 utimos casos las formulas de derivacion >> pretty(F2) n - 1 n x --------- n 1/2 2 (x ) >> ans ans = n*x^(n - 1) >> pretty (ans) n - 1 n x
jueves, 10 de octubre de 2013
Calculo de Limites en Matlab
Hace un tiempo atrás cursando introducción al calculo en la universidad los temas de limites, limites laterales, limites en el infinito, continuidad. fueron un dolor de cabeza, aun que debo confesar que ese dolor de cabeza aumento demasiado cuanto curse ecuaciones Diferenciales. Buscando un poco aligerar la carga de algún chico que curse estas materias prepare una serie de post referentes a calculo utilizando Matlab.
>> %ejemplo de un limite en Matlab >> syms x >> limit (x^2,x,3) ans = 9 >> %ahora calcularemos un limite en el infinito >> limit(sqrt(x^2+1),x,inf) ans = Inf >> %otro ejemplo muy poco conocido es el calculo de los limites laterales en matlab >> limit(tan(x),x,pi/2,'left') %limite por la izquierda ans = Inf >> limit(tan(x),x,pi/2,'right') %limite por la drecha ans = -Inf >> % en este caso los limites tando de la derecha e izquierda no son iguales entonces >> %% la funcion no es continua >>
martes, 24 de septiembre de 2013
martes, 17 de septiembre de 2013
Método de Gauss-Jordan en Matlab (en forma de función)
function respuesta=gauss(a,b) %%---obtener la solcuion de un sistema de ecuaciones por el metod de gauss %%------------------------------------------------------------------------ % a= matriz cuadrada con los coefcientes del sistema % b= los coeficientes de las igualdades de las ecuaciones del sistema %*************************************************************************** variables=length(a); for i=1:variables aux=1/a(i,i); %*******Convirtiendo en 1 el elemnto de la matriz identidad****** b(i)=b(i)*aux; for j=1:variables a(i,j)=a(i,j)*aux; end %//*******eliminando las filas precedentes****************** for j=1:i-1 aux=-1*a(j,i); b(j)=b(j)+b(i)*aux; for k=1:variables a(j,k)=a(j,k)+aux*a(i,k); end end %//*******eliminando las filas posteriores****************** for j=i+1:variables aux=-1*a(j,i); b(j)=b(j)+b(i)*aux; for k=1:variables a(j,k)=a(j,k)+aux*a(i,k); end end end disp(a); respuesta=b;
viernes, 13 de septiembre de 2013
Factor LU de matriz-- en Matlab
ejecutando la funcionfunction [L,U]= factorlu (A) n=length(A); U=A; L=eye(n); for p=1:n for q = p+1:n L(q,p)=U(q,p)/U(p,p); U(q,p:n)=U(q,p:n)-U(p,p:n)*L(q,p); end end
>> A = [1 2 2; 4 4 2; 2 6 4]; >> [L,U]=factorlu(A) L = 1.0000 0 0 4.0000 1.0000 0 2.0000 -0.5000 1.0000 U = 1 2 2 0 -4 -6 0 0 -3
miércoles, 4 de septiembre de 2013
jueves, 29 de agosto de 2013
jueves, 22 de agosto de 2013
miércoles, 14 de agosto de 2013
orderseek--Encontrar el orden de una reacción Química en Matlab
Este pequeño programa hecho en Matlab nos sirve para hallar el orden de una reacción química, cabe señalar que este programa no es creación mía, pero lo estoy usando como punto de partida para crear un propio programa ya que en el caso de reacciones químicas tenemos muchos casos como son, volumen constante, volumen Variable, Reversibles, etc.
jueves, 8 de agosto de 2013
Python para Bioinformatica — Introducción al Comando Seq (parte 2)
Python para BioInformatica introducción al comando Seq (parte 1)
- Cortando una Secuencia.
este tipo de conversión es muy útil cuando tenemos un archivo de texto plano o introducimos mediante un programa nuestra secuencia.
-Transcripción y Translación
- Cortando una Secuencia.
-Convertir de String a Secuencia>>> from Bio.Seq import Seq >>> from Bio.Seq import IUPAC >>> secuencia = Seq ("ACGCTAGCTAGCTCGCAACGCTCGAACGCTCG") >>> len(secuencia) 32 >>> secuenciacorta = secuencia[5:10] >>> secuenciacorta Seq('AGCTA', Alphabet())
este tipo de conversión es muy útil cuando tenemos un archivo de texto plano o introducimos mediante un programa nuestra secuencia.
>>> secuencia = input('introduce tu secuencia: ') introduce tu secuencia: AGCTGCGTG >>> secuencia 'AGCTGCGTG' >>> type(secuencia) <class 'str'> >>> Secuencia2 = Seq(secuencia) >>> type(Secuencia2) <class 'Bio.Seq.Seq'> >>> ## se puede hacer en la misma linea >>> SECUENCIA = Seq(input('introduce tu secuencia: ')) introduce tu secuencia: AGCTCGACGCT >>> type(SECUENCIA) <class 'Bio.Seq.Seq'>
-Transcripción y Translación
>>> secuencia = Seq ("ACGCTAGCTAGCTCGCAACGCTCGAACGCTCG") >>> transcripcion =secuencia.transcribe() >>> transcripcion Seq('ACGCUAGCUAGCUCGCAACGCUCGAACGCUCG', RNAAlphabet()) >>> traslacion = secuencia.translate() >>> traslacion Seq('TLASSQRSNA', ExtendedIUPACProtein())
lunes, 5 de agosto de 2013
Diagrama Liquido- Vapor en un proceso Isobarico-- usando Matlab
El modelo de Wilson permite que el programa para tener en cuenta la desviación del comportamiento ideal en la fase líquida. El usuario debe introducir bajo presiones moderadas ya que el término de corrección a alta presión no está incluido.
martes, 30 de julio de 2013
"Matlab for Genius", Busqueda de la solucion de una Ecuacion--- Método Grafico
Hace unos días atrás me enviaron una consulta de como encontrar la solución de una ecuación en matlab.
supongamos que tenemos la siguiente ecuación.
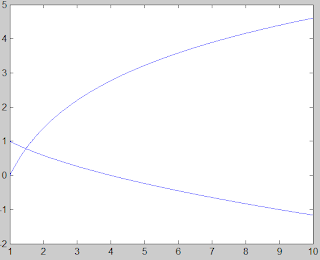
2log (x) = 2 - (x)^(1/2)
en la que necesitaros encontrar el punto en el que se encuentra nuestra solución, para ello usaremos en esta entrega el método gráfico.
el gráfico nos queda de la siguiente manera, donde el punto de intersección es la solución.>> %declaramos un vector x donde acotaremos nuestra solucion >> x = 1:0.01:10; >> % formaremos dos variables en las que estaran nuestras ecuaciones >> f1 = 2*log(x); >> f2 = 2 -x.^(1/2); >> plot(x,f1) >> hold on >> plot(x,f2) >> hold off
Multiples estados estacionarios, estudio de un Catalizador
El problema catalizador adiabática se presenta en el campo de la ingeniería química. Si cinética de las reacciones químicas dentro de un cuerpo de catalizador sólido se ven influidas por la transferencia de masa múltiples estados estacionarios son posibles para una cierta gama de los parámetros que rigen: número de Arrhenius, número Prater y módulo de Thiele.
lunes, 29 de julio de 2013
valtitu.py 2.0 (Programa de valoración y titulacion de Soluciones )
Hace unos días atrás publicamos la primera versión de programa de valoración de soluciones continuación les dejo la segunda versión, en esta hacemos uso de la librería tkinter.
el código fuente es el siguiente:
el código fuente es el siguiente:
##Programa de valoracion de Soluciones vercion 2 #### usando la ecuancion C1V1 = C2V2 ##### es necesario tener python 3.3 y la libreria tkinter ###### hecho por israel Nuñez ####### Universidad Autonoma Metropolitana ### isrant.blogspot.com ##### mexico D.F from tkinter import* from tkinter import messagebox import math def variables(e): global cas var = lb.curselection() var1 = tuple(('0',)) var2 = tuple(('1',)) var3 = tuple (('2')) var4 = tuple (('3')) if var == var1: ##calculando C1 cas = 1 texto=Label(ventana,text='V2') texto.place(bordermode = OUTSIDE, height=20, width =100, x = 300, y = 60) texto = Label(ventana, text = "V1") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto = Label(ventana, text = "C2") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) textores2 = Label(ventana, text = "C1") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) elif var == var2: ##calculando C2 cas = 2 texto=Label(ventana,text='V2') texto.place(bordermode = OUTSIDE, height=20, width =100, x = 300, y = 60) texto = Label(ventana, text = "V1") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto = Label(ventana, text = "C1") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) textores2 = Label(ventana, text = "C2") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) elif var == var3: cas = 3 ##calculando V1 texto=Label(ventana,text='V2') texto.place(bordermode = OUTSIDE, height=20, width =100, x = 300, y = 60) texto = Label(ventana, text = "C1") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto = Label(ventana, text = "C2") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) textores2 = Label(ventana, text = "V1") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) elif var ==var4: cas = 4 ##calculando V2 texto=Label(ventana,text='V1') texto.place(bordermode = OUTSIDE, height=20, width =100, x = 300, y = 60) texto = Label(ventana, text = "C1") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto=Label(ventana,text='C2') texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) textores2 = Label(ventana, text = "v2") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) else: messagebox.showerror('Error','Fuera de Rango') ##operacion del boton calcular def calcular(): global cas variable1 = vari1.get() variable2 = vari2.get() variable3 = vari3.get() if cas == 1: v2=float(variable1) v1= float(variable2) c2= float(variable3) ##operacion resultado = (c2*v2)/v1 rest.set(resultado) elif cas == 2: v2=float(variable1) v1 = float(variable2) c1 = float(variable3) resultado = (c1*v1)/v2 rest.set(resultado) elif cas == 3: v2=float(variable1) c1 = float(variable2) c2 = float(variable3) resultado =(c2*v2)/c1 rest.set(resultado) elif cas == 4: v1 = float(variable1) c1 = float(variable2) c2 = float(variable3) resultado = (c1 *v1)/c2 rest.set(resultado) else: messagebox.showerror('Error','Selecciona una Variable') def acerca(): messagebox.showinfo('acerca de','Desarrollado por Israel Nuñez') ventana = Frame (height = 300, width = 600) ventana.pack(padx =10, pady = 10) variable1 = DoubleVar() variable2 = DoubleVar() variable3 = DoubleVar() cas = 0 rest = StringVar() #probando listbox textolb = Label(ventana, text = "Seleccione Variable") textolb.place(bordermode = OUTSIDE, height = 20, width = 150, x= 100, y= 20) lb = Listbox(ventana) lb.insert(1,"C1") lb.insert(2,"C2") lb.insert(3,"V1") lb.insert(3,"V2") lb.bind('<>' ,variables) lb.place(bordermode = OUTSIDE, height = 100, width = 150, x = 100, y= 40) #boton calcular boton = Button(ventana, text = "calcular",command= calcular ) boton.place(bordermode = OUTSIDE, height = 30, width =80, x=350, y = 200) #boton acercade boton2 = Button(ventana, text ="acerca de...", command = acerca) boton2.place (bordermode = OUTSIDE , height = 30, width = 80, x= 450, y= 200) #texto de presentacion texto=Label(ventana,text='Variable 1') texto.place(bordermode = OUTSIDE, height=20, width =100, x = 300, y = 60) texto = Label(ventana, text = "Variable 2") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto = Label(ventana, text = "Variable 3") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) #Entrada de Datos vari1 = Entry(ventana, textvariable =variable1) vari1.place(bordermode= OUTSIDE, height= 30, width = 100, x= 400, y= 100) vari2 = Entry(ventana,textvariable=variable2) vari2.place(bordermode= OUTSIDE, height= 30, width = 100, x= 400, y= 140) vari3 = Entry(ventana, textvariable = variable3) vari3.place(bordermode = OUTSIDE, height = 30, width = 100, x= 400, y= 60) #para mostrar resultados textores = Label(ventana, text = "Resultado") textores.place(bordermode = OUTSIDE, height = 20, width = 150, x= 100, y= 200) textores2 = Label(ventana, text = "Variable") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) res = Label(ventana,textvariable = rest, fg = "blue",bg = "yellow") res.place(bordermode = OUTSIDE, height = 20, width = 200, x = 200, y = 250)
miércoles, 24 de julio de 2013
Manejo de Listbox en Python 3.x. Usando Tkinter
Como ven es una pequeña aplicacion desarrollada en Python usando Tkinter en especial me enfoco en el uso de los Listbox, como veran es la aplicacion de todos los posibles casos del teorema de pitagoras, la funcion que controla el Listbox tiene por nombre hola, para que la identifiquen.
## teoremas para triangulos #pitagoras9 from tkinter import* from tkinter import messagebox import math def hola(e): global cas var = lb.curselection() var1 = tuple(('0',)) var2 = tuple(('1',)) var3 = tuple (('2')) if var == var1: ##calculando cateto opuesto cas = 1 texto = Label(ventana, text = "Hipotenusa") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto = Label(ventana, text = "C. Adyacente") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) textores2 = Label(ventana, text = "C. Opuesto") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) elif var == var2: ##calculando cateto Adyacente cas = 2 texto = Label(ventana, text = "Hipotenusa") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto = Label(ventana, text = "C. Opuesto") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) textores2 = Label(ventana, text = "C. Adyacente") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) elif var == var3: cas = 3 ##calculando hipotenusa texto = Label(ventana, text = "C. Opuesto") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto = Label(ventana, text = "C. Adyacente") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) textores2 = Label(ventana, text = "Hipotenusa") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) else: print ('Fuera de Rango') ##operacion del boton calcular def calcular(): global cas variable1 = vari1.get() variable2 = vari2.get() if cas == 1: h=float(variable1) ca = float(variable2) ##operacion resultado = math.sqrt((h*h) - (ca*ca)) rest.set(resultado) elif cas == 2: h=float(variable1) co = float(variable2) resultado = math.sqrt((h*h) - (co*co)) rest.set(resultado) elif cas == 3: co=float(variable1) ca = float(variable2) resultado = math.sqrt((co*co) + (ca*ca)) rest.set(resultado) else: messagebox.showerror('Error','Selecciona una Variable') ventana = Frame (height = 300, width = 600) ventana.pack(padx =10, pady = 10) variable1 = DoubleVar() variable2 = DoubleVar() cas = 0 rest = StringVar() #probando listbox textolb = Label(ventana, text = "Seleccione Variable") textolb.place(bordermode = OUTSIDE, height = 20, width = 150, x= 100, y= 20) lb = Listbox(ventana) lb.insert(1,"Cateto Opuesto") lb.insert(2,"Cateto Abyacente") lb.insert(3,"Hipotenusa") lb.bind('<>' ,hola) lb.place(bordermode = OUTSIDE, height = 70, width = 150, x = 100, y= 40) #boton calcular boton = Button(ventana, text = "calcular",command= calcular ) boton.place(bordermode = OUTSIDE, height = 30, width =80, x=350, y = 200) #texto de presentacion texto = Label(ventana, text = "Variable 1") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 100) texto = Label(ventana, text = "Variable 2") texto.place(bordermode = OUTSIDE, height = 20, width = 100, x= 300, y= 140) #Entrada de Datos vari1 = Entry(ventana, textvariable =variable1) vari1.place(bordermode= OUTSIDE, height= 30, width = 100, x= 400, y= 100) vari2 = Entry(ventana,textvariable=variable2) vari2.place(bordermode= OUTSIDE, height= 30, width = 100, x= 400, y= 140) #para mostrar resustados textores = Label(ventana, text = "Resultado") textores.place(bordermode = OUTSIDE, height = 20, width = 150, x= 100, y= 200) textores2 = Label(ventana, text = "Variable") textores2.place(bordermode = OUTSIDE, height = 20, width = 150, x = 50, y = 250) res = Label(ventana,textvariable = rest, fg = "blue",bg = "yellow") res.place(bordermode = OUTSIDE, height = 20, width = 200, x = 200, y = 250)
Suscribirse a:
Comentarios (Atom)